はじめに

本ページでは, その他の取り組みページで実行可能な斜面安定シミュレーションと, 簡単2次元弾塑性FEMの計算結果について,
その妥当性を評価することを目的として, 蔡ら¹⁾の論文の計算結果と比較を行う.
各物性値については, 論文の内容から取得した. ただし, モデルの座標については, 論文中に詳細な記載がないため, 目測で取得した.

1. 例1

モデル詳細

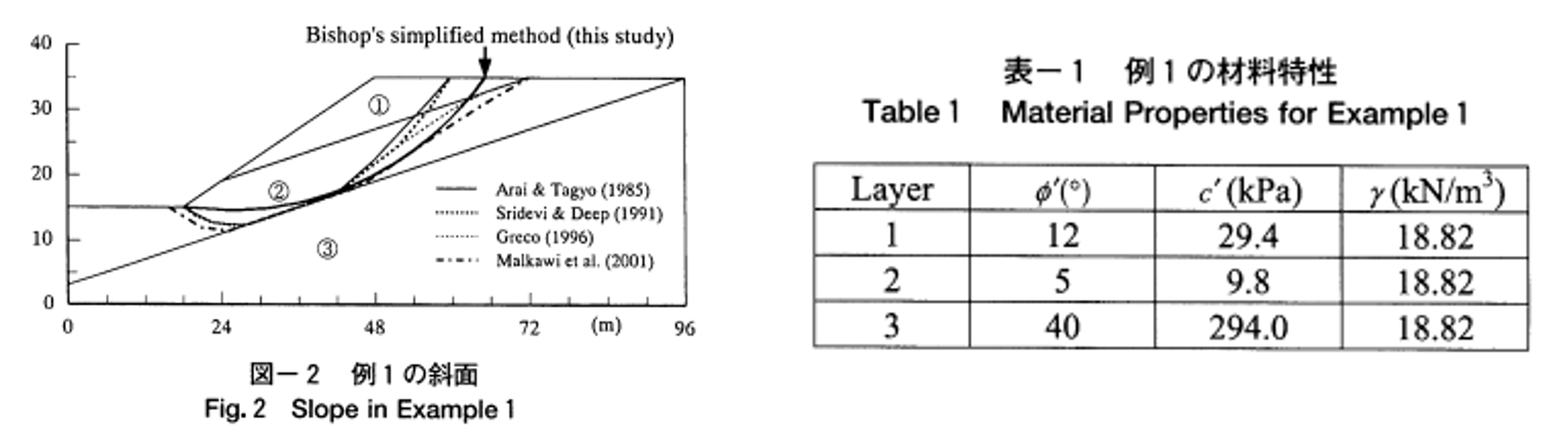
モデルと各物性値は図1-1の通りである.

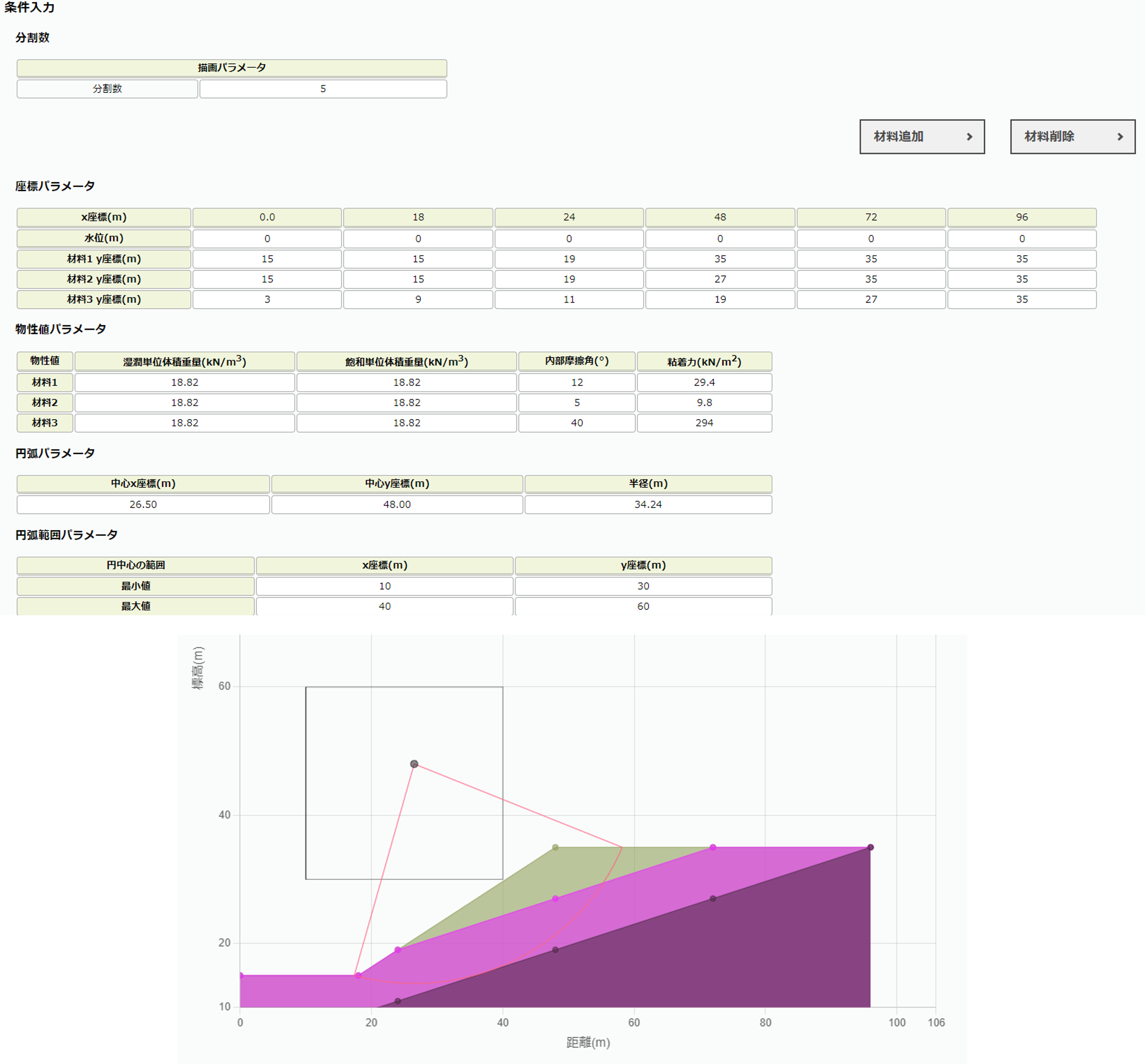
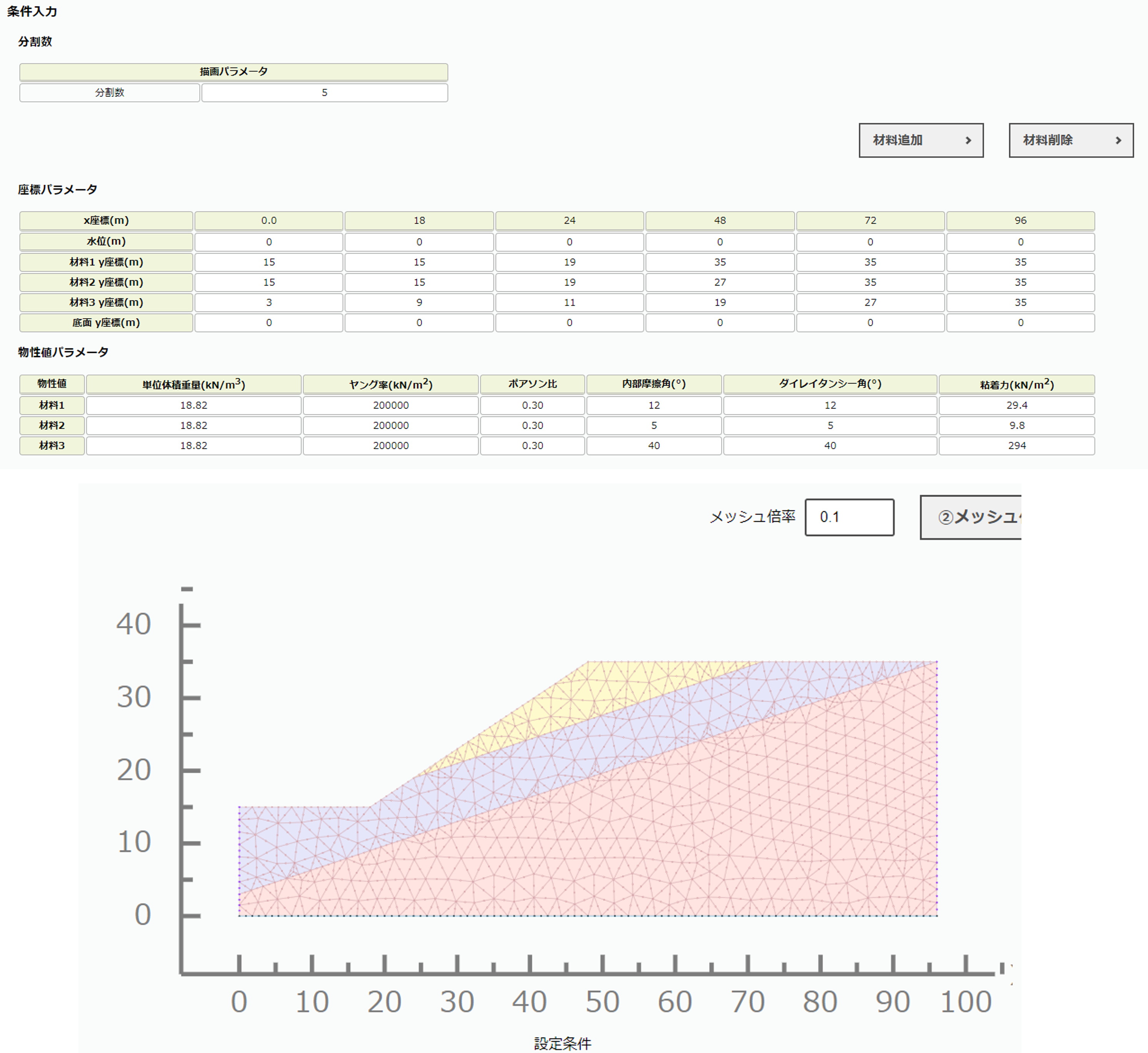
本サイトの斜面安定計算と2次元弾塑性では図1-2, 図1-3の通りモデル化した.

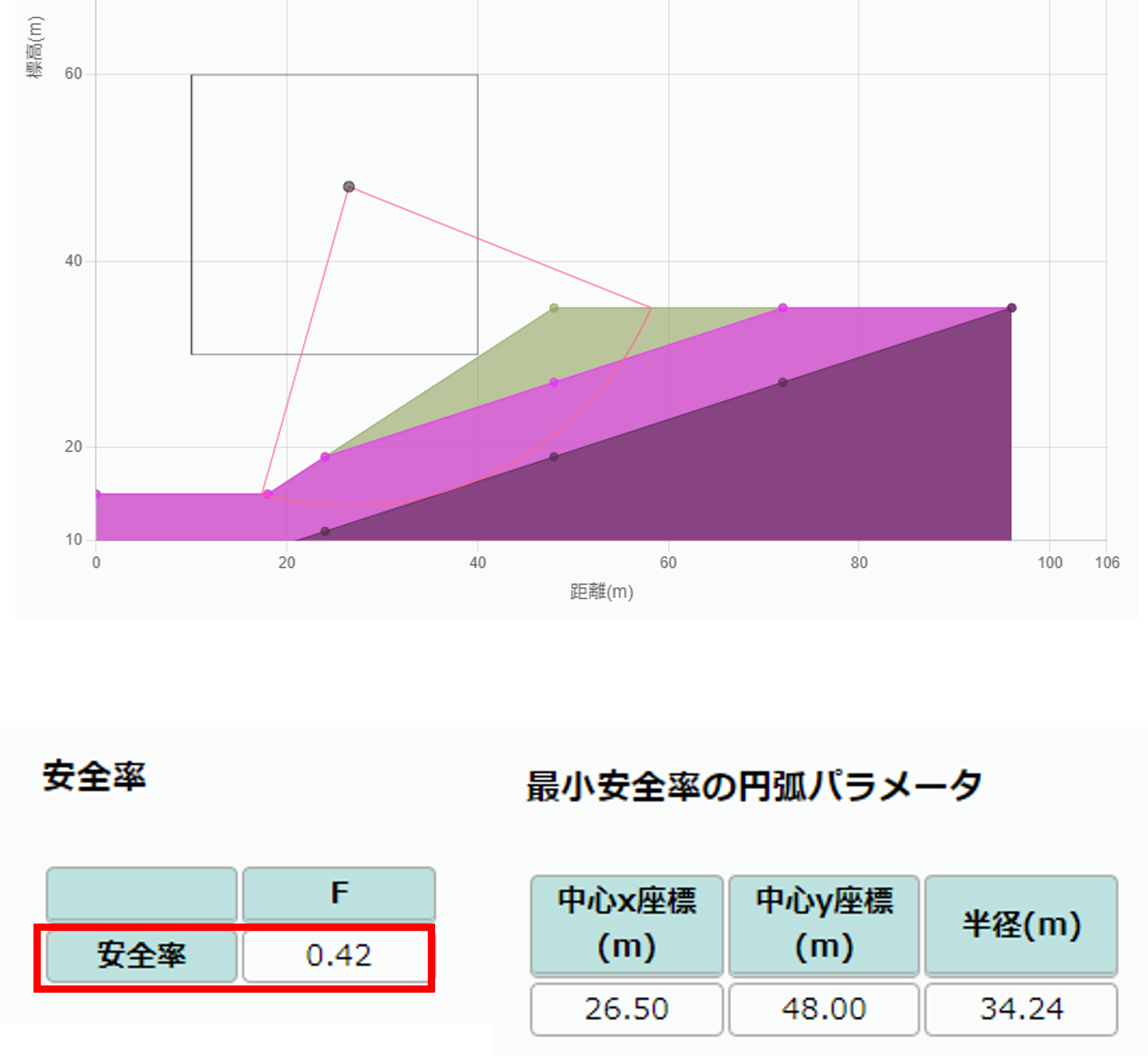
シミュレーション結果

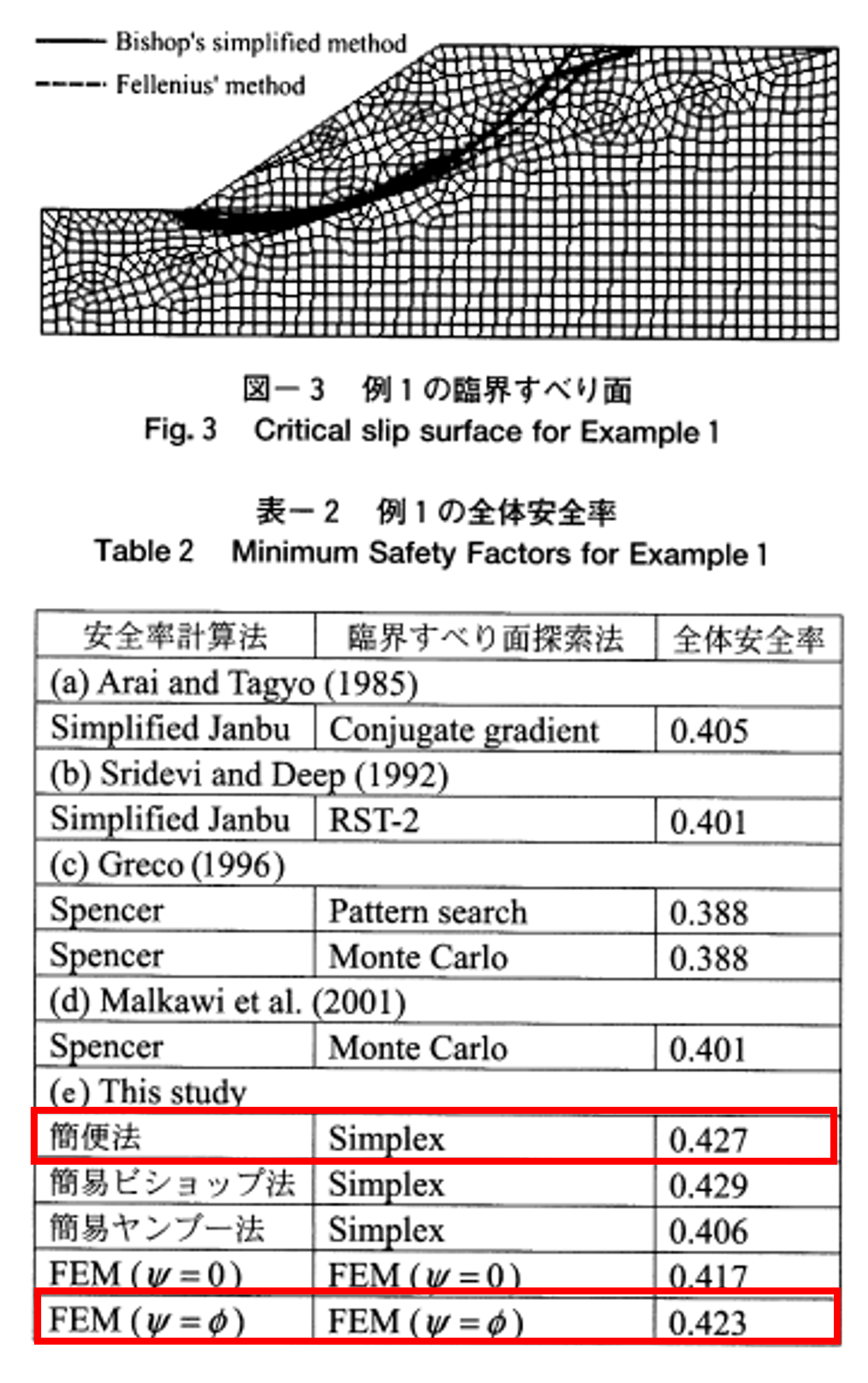
蔡ら(2003)の結果と本シミュレーション結果を図1-4~1-6に示す. 斜面安定計算は, 修正フェレニウス法の結果が論文中になかったため, 簡便法と比較する.
比較した結果, 図1-4より斜面安定計算の安全率は論文が0.427, 図1-5より本シミュレーション結果が0.42とおおよそ一致していることがわかる.
さらに, 円弧の形状は, 図1-4中のFellenius'methodと本シミュレーション結果いずれも, 2層と3層の境界を通るような結果となっており, これもおおよそ一致した.
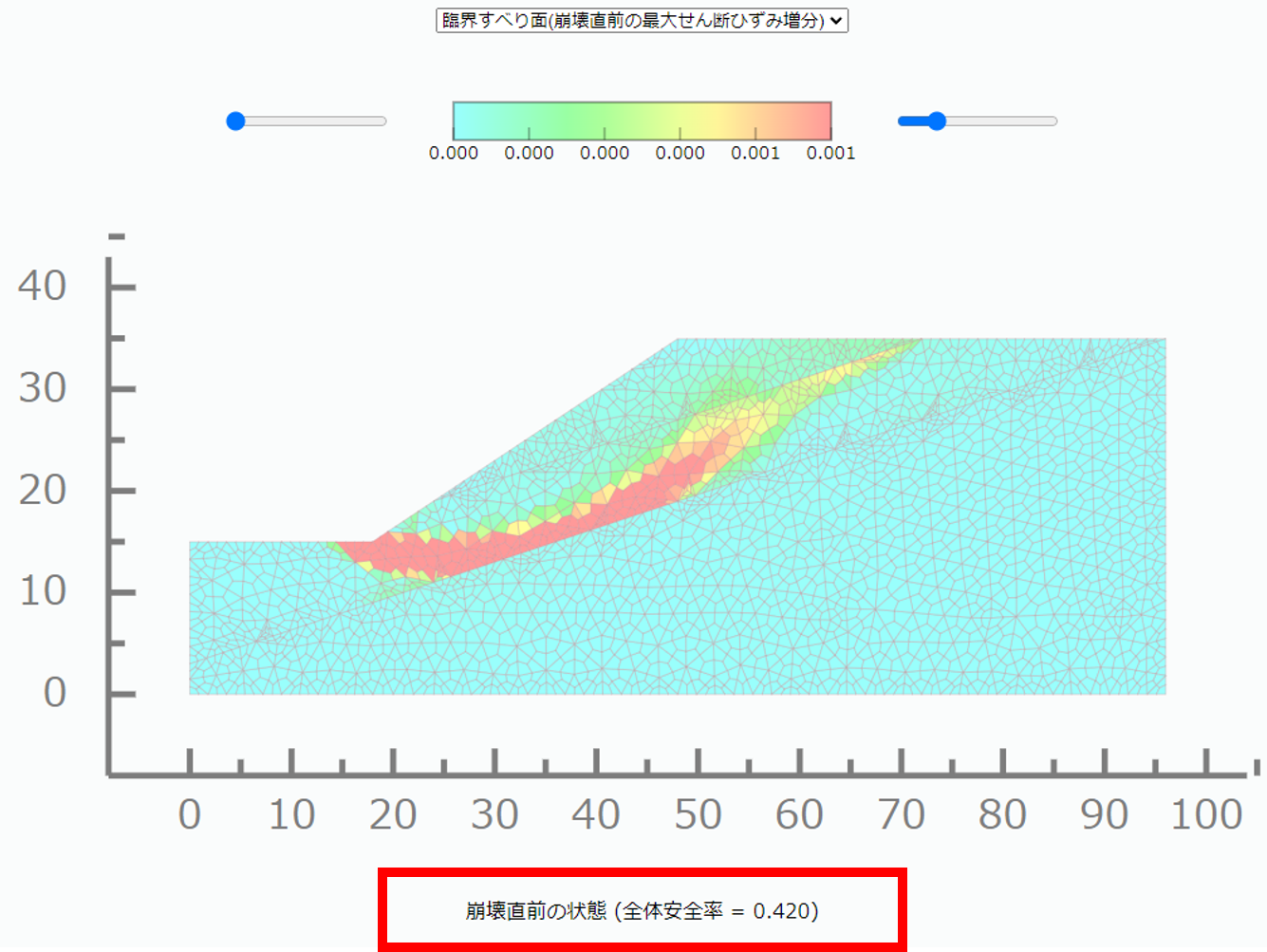
一方, FEMの安全率は, 図1-4より論文が0.423, 図1-6より本シミュレーション結果が0.42とおおよそ一致していることがわかる.
さらに, 臨界すべり面の形状は, 2層と3層の境界を通るような結果となっており, これもおおよそ一致した.

2. 例2

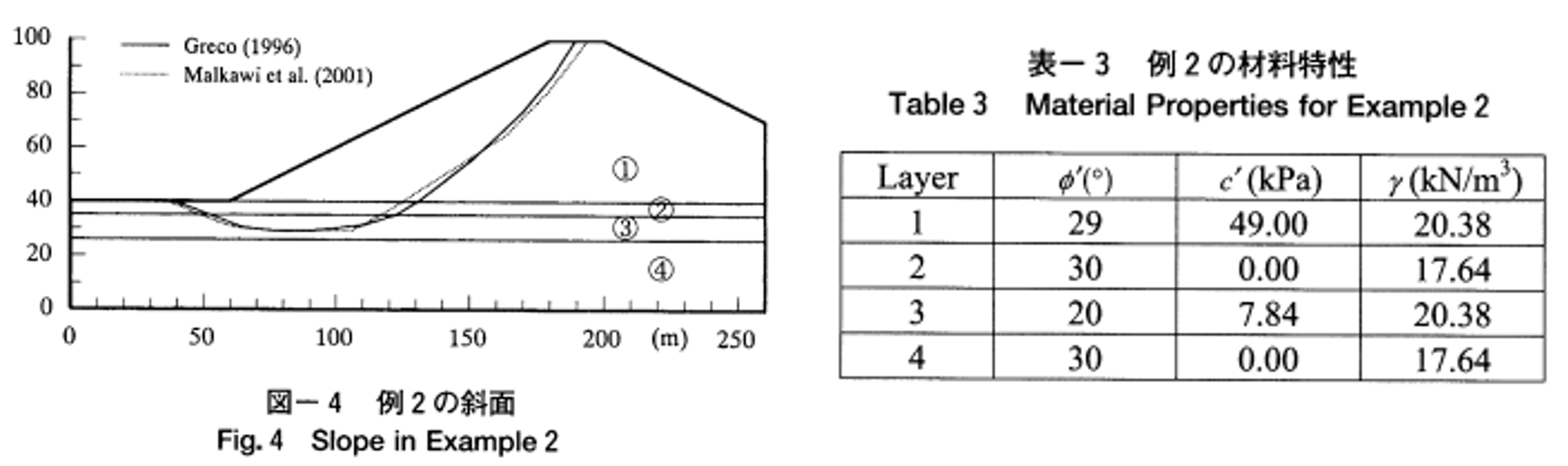
モデル詳細

モデルと各物性値は図2-1の通りである.

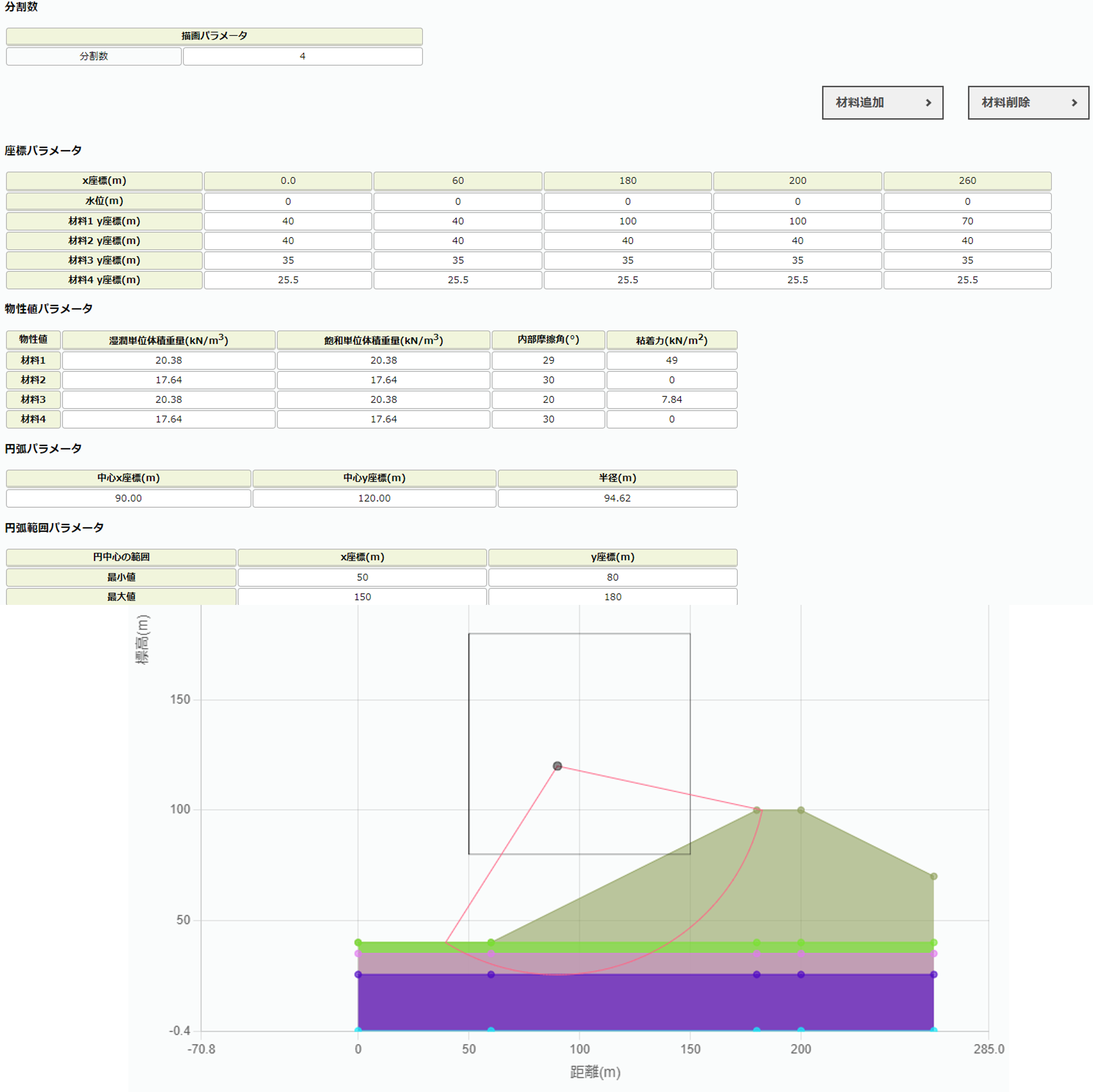
本サイトの斜面安定計算と2次元弾塑性では図2-2, 図2-3の通りモデル化した.

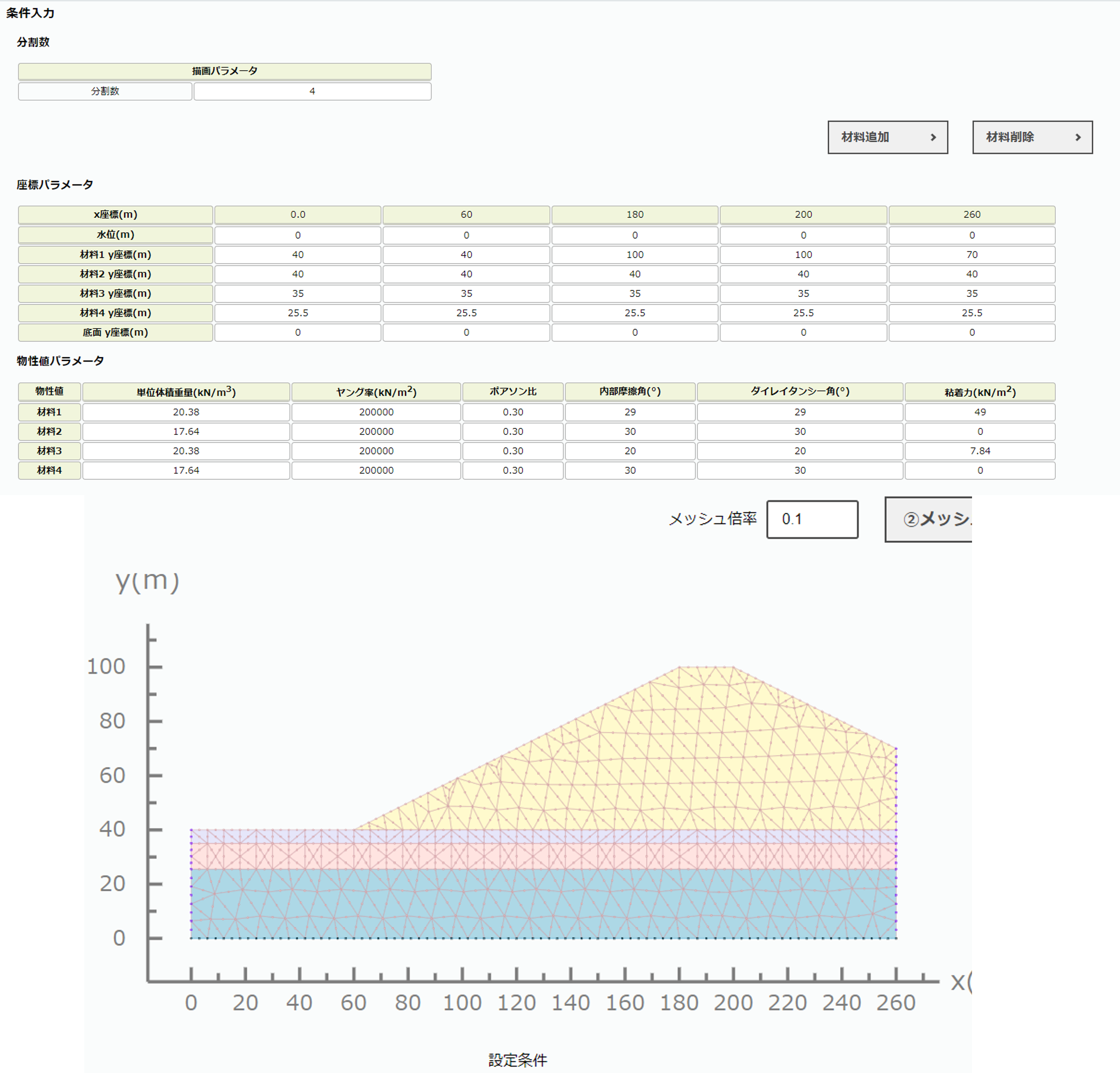
シミュレーション結果

蔡ら(2003)の結果と本シミュレーション結果を図2-4~2-6に示す. 斜面安定計算は, 修正フェレニウス法の結果が論文中になかったため, 簡便法と比較する.
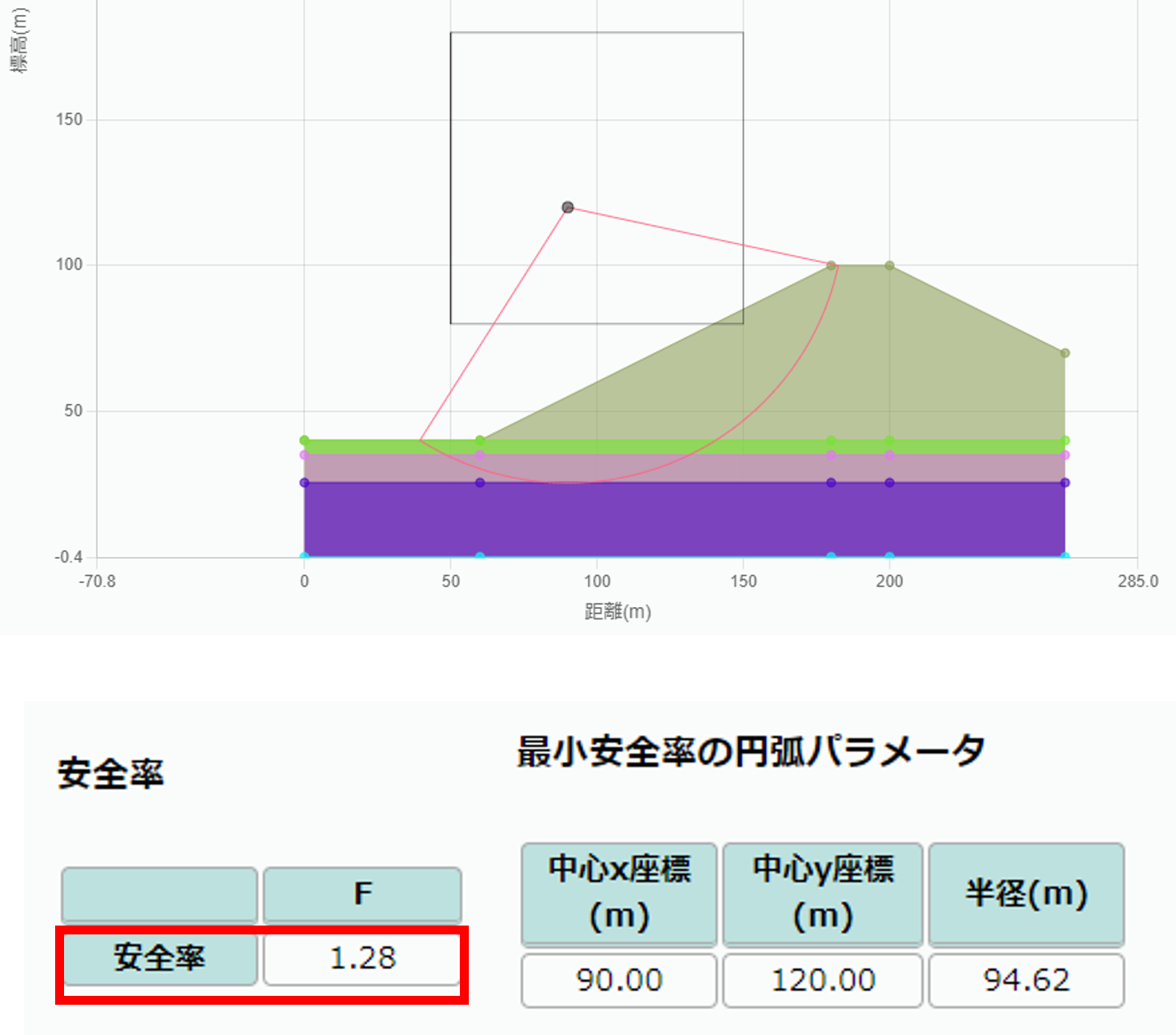
比較した結果, 図2-4より斜面安定計算の安全率は論文が1.276, 図2-5より本シミュレーション結果が1.28とおおよそ一致していることがわかる.
さらに, 円弧の形状は, 他の手法になるが, 図2-4中のBishiop's simplified methodと本シミュレーション結果いずれも, 3層と4層の境界を通るような結果となっており, これもおおよそ一致した.
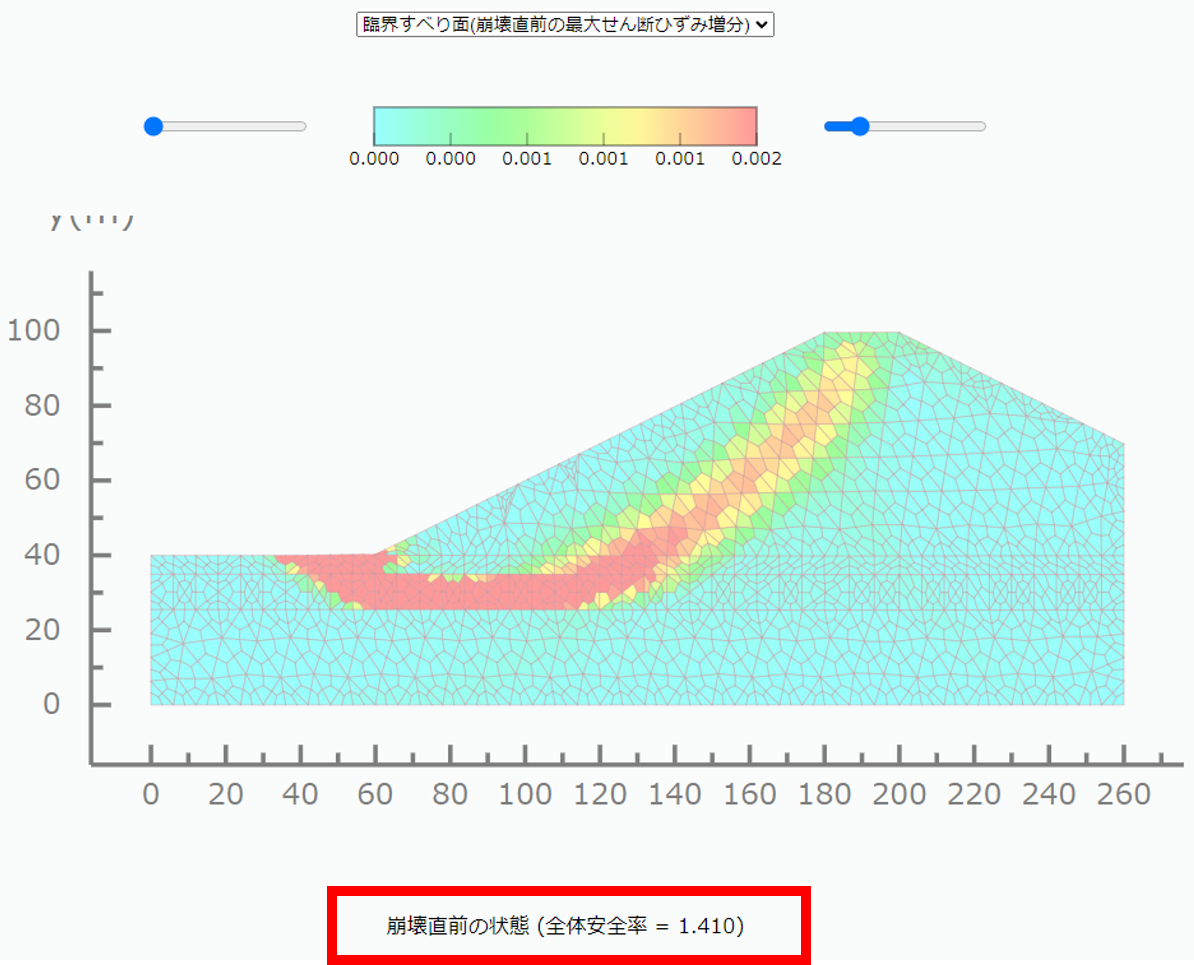
一方, FEMの安全率は, 図2-4より論文が1.403, 図2-6より本シミュレーション結果が1.410とおおよそ一致していることがわかる.
さらに, 臨界すべり面の形状は, 3層と4層の境界を通るような結果となっており, これもおおよそ一致した.

3. 例3

モデル詳細

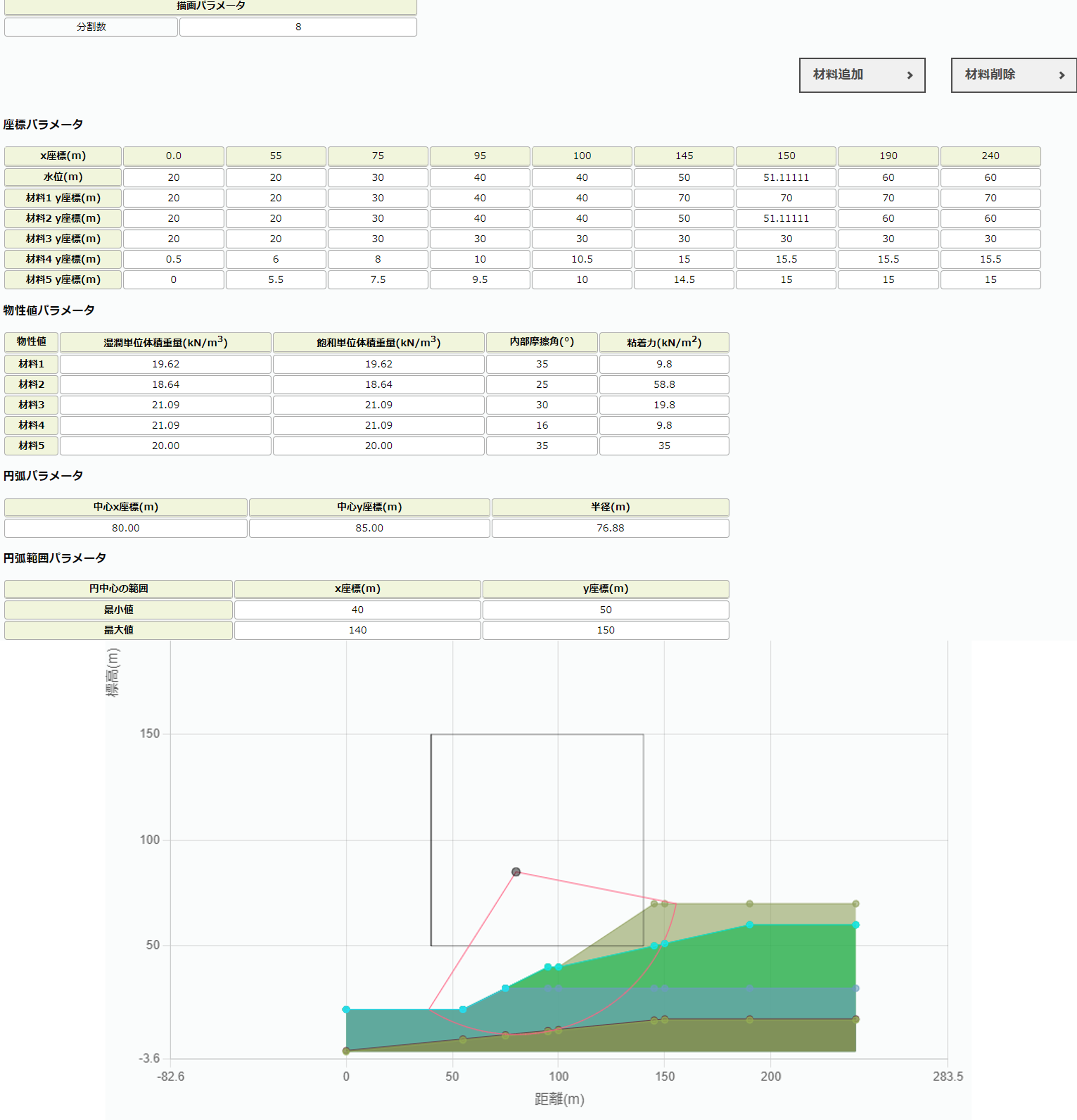
モデルと各物性値は図3-1の通りである.

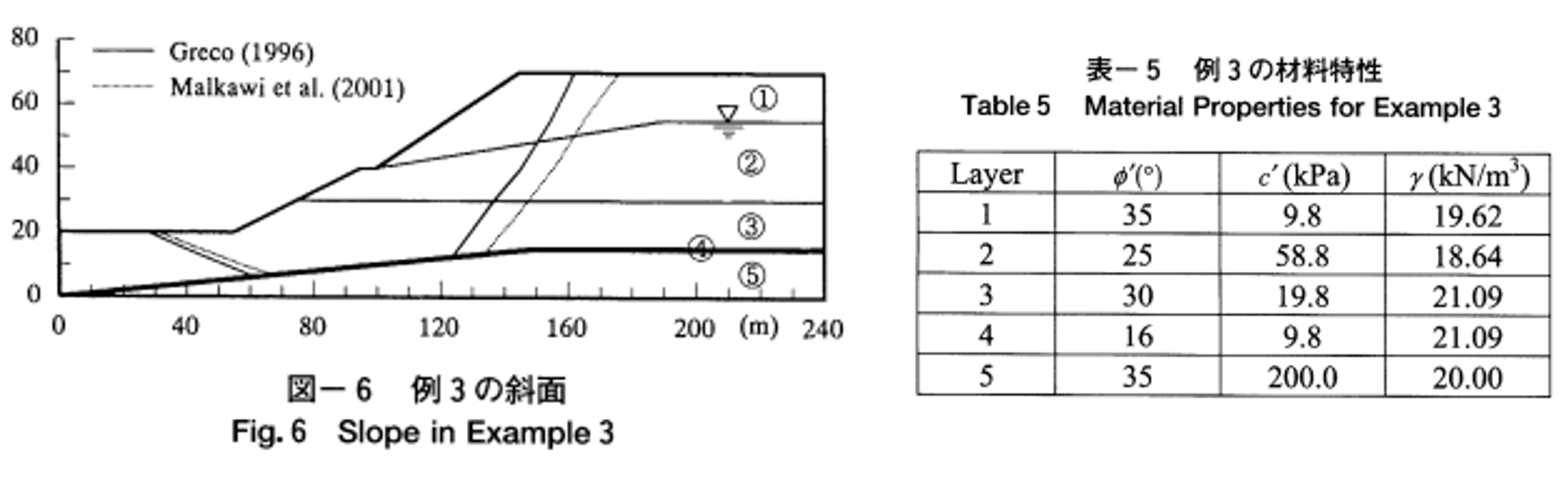
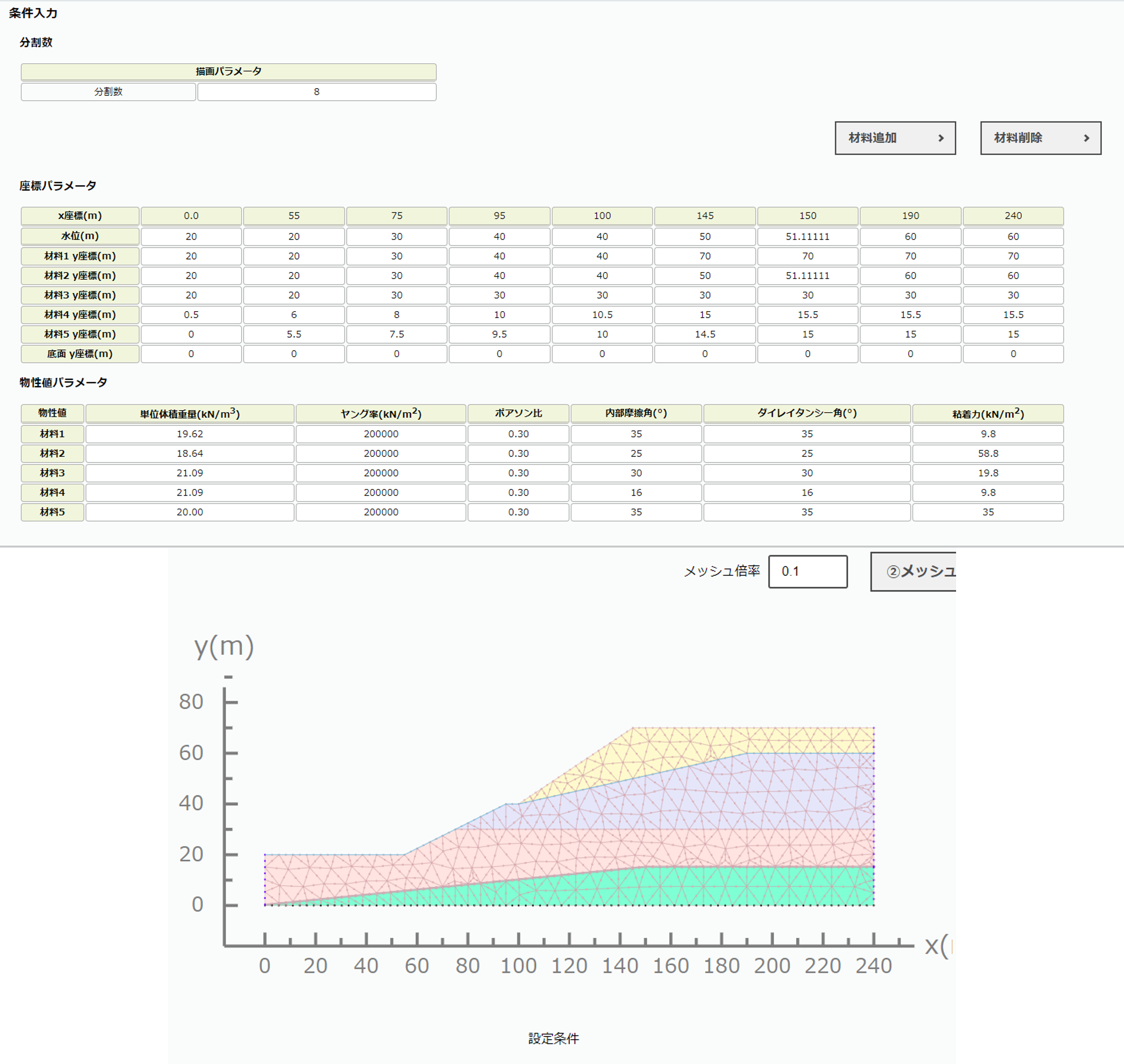
本サイトの斜面安定計算と2次元弾塑性では図3-2, 図3-3の通りモデル化した.

シミュレーション結果

蔡ら(2003)の結果と本シミュレーション結果を図3-4~3-6に示す. 斜面安定計算は, 修正フェレニウス法の結果が論文中になかったため, 結果の検証のみとする.
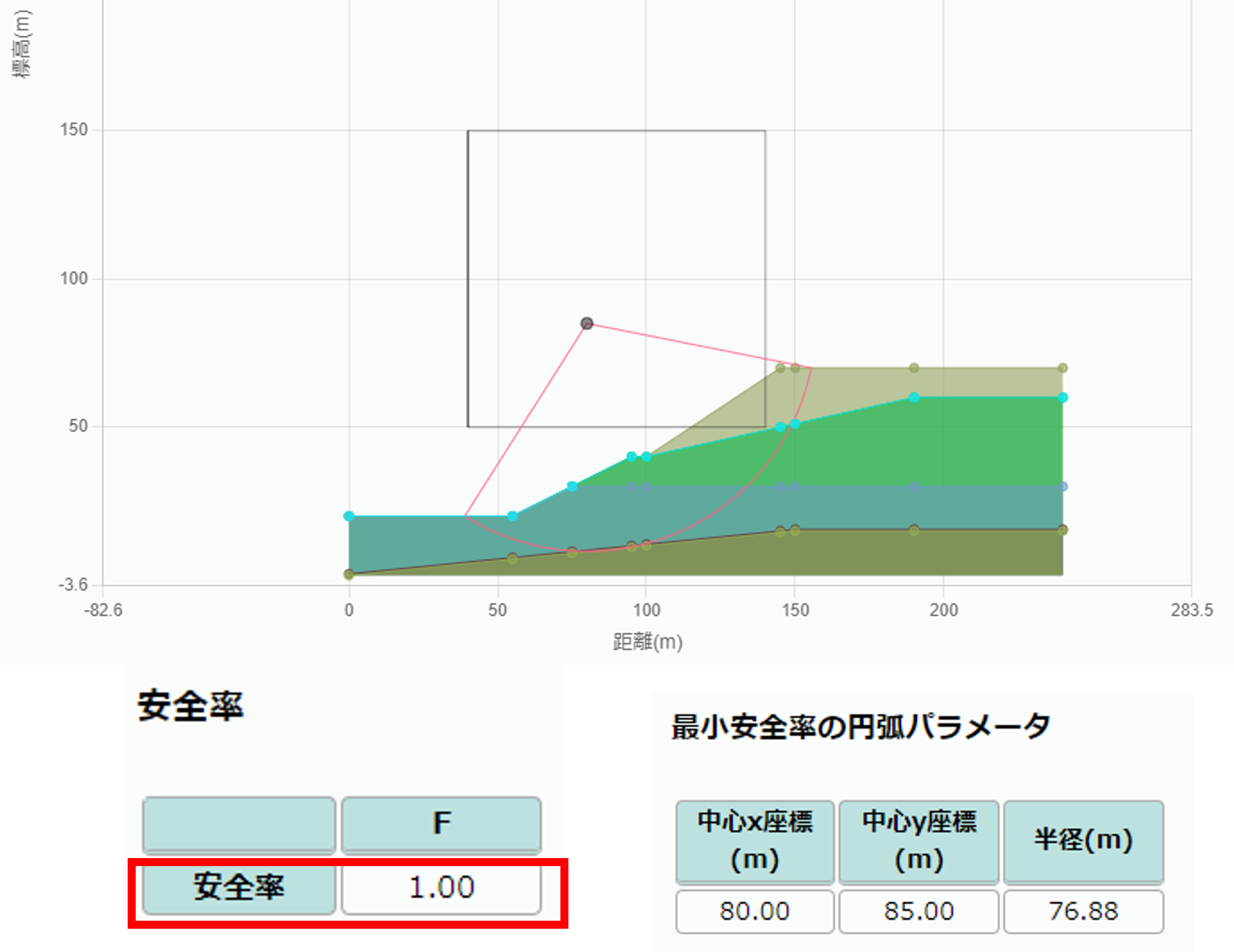
図3-5より斜面安定計算の安全率は, 本シミュレーション結果が1.00となった. 図3-4の簡便法と値が大きく異なるのは水圧の計算方法が異なるのが原因として考えられる.
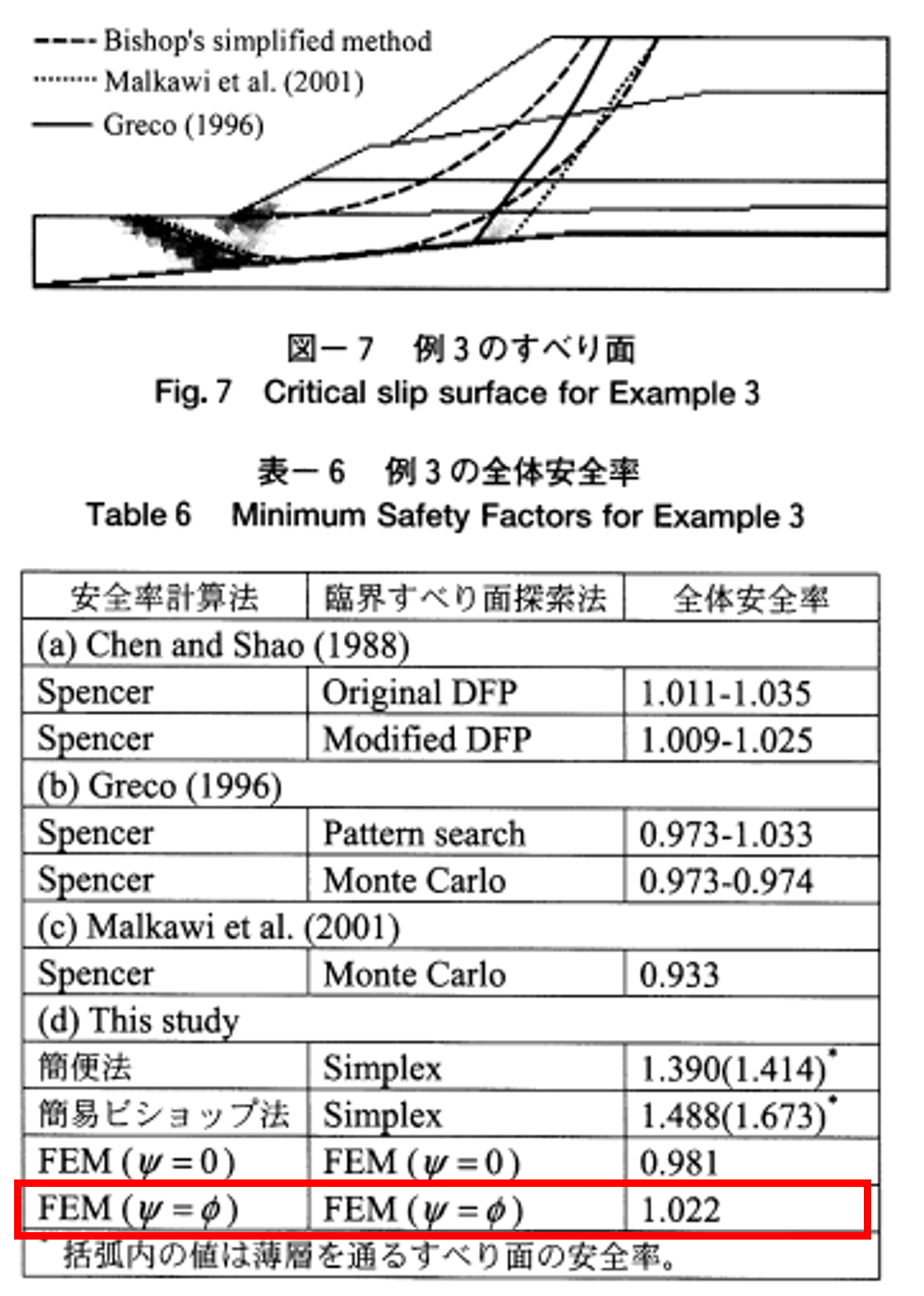
図3-4のSpencer法やFEMの安全率と比較すると, 本シミュレーション結果ではおおよそ近い値が得られていることがわかる.
さらに, 円弧の形状は, 他の手法になるが, 図3-4中のBishiop's simplified methodと本シミュレーション結果いずれも, 弱層である4層を通るような結果となっており,おおよそ一致した.
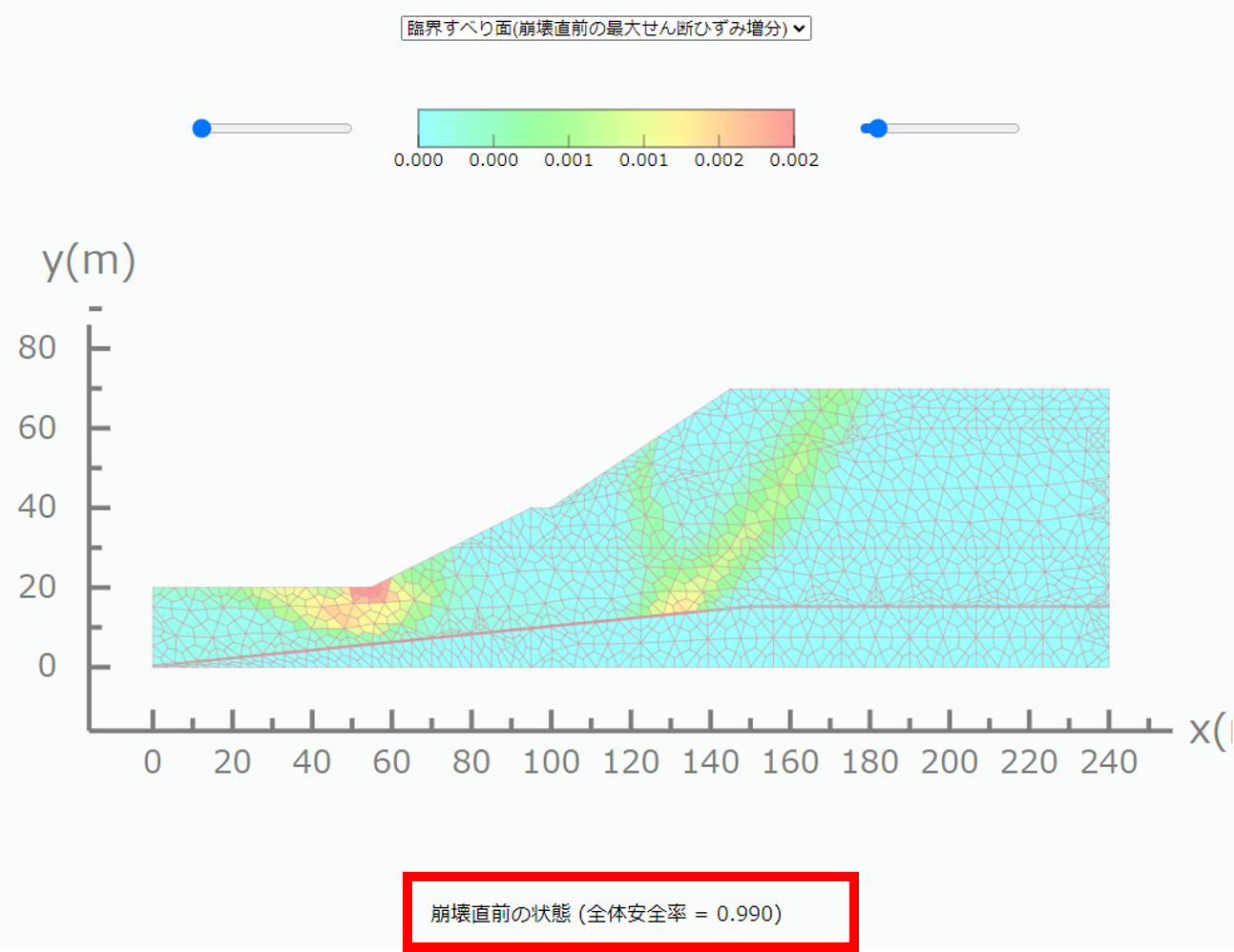
一方, FEMの安全率は, 図3-4より論文が1.022, 図3-6より本シミュレーション結果が0.99とおおよそ一致していることがわかる.
さらに, 臨界すべり面の形状は, 弱層である4層の境界を通るような結果となっており, これもおおよそ一致した.

おわりに

本ページでは, その他の取り組みページで実行可能な斜面安定シミュレーションと, 簡単2次元弾塑性FEMの計算結果について, 蔡ら(2003)の論文の計算結果との比較を行った.
比較した結果斜面安定計算, 2次元弾塑性FEMともに論文と近い値が得られることがわかり, 本シミュレーションの妥当性がある程度示されたと考える.
安全率の細かい違いについては, 計算方法の違い(メッシュの切り方, 収束判定等), 丸め誤差等の計算処理の違いが考えられるため, より精度を上げるためには, それらの改善が必要であると考える.
また, FEMについては, 応力やひずみの結果の比較を行っていないため, 本シミュレーションの妥当性の評価についてはこれらについても別途検討する必要がある.